오늘부터 다시 수리통계학을 복습해보려 한다.
애들레이드 대학(THE UNIVERSITY OF ADELAIDE)의 수리통계학 강의노트를 이용하여 공부할 계획이다.
잘못된 부분이 있다면 댓글을 남겨주길 바란다.
오늘은 이산형 확률 분포에 대해 얘기를 해보자.
1. 베르누이 분포(Bernouli distribution)
결과가 상호배반적인 두 종류(e.g. 성공, 실패)로만 구성된 실험의 성공 확률이 시행마다 일정하고, 각 시행이 서로 독립적일 때 베르누이 시행이라고 한다.
- Parameter : $ 0 \leq p \leq 1$
- Possible values : {0,1}
- x의 p.m.f.
$$ f(x) = p^{x}(1-p)^{1-x}, x=0,1 $$
이때 $X$는 모수 $p$인 베르누이 분포를 갖는다고 한다.
- $E(X)=p$
- $Var(X)=p(1-p)$
- $M_{x}(t)=1+p(e^{t}-1)$
2. 이항분포(Binomial distribution)
성공확률이 $p$인 베르누이 시행을 $n$번 반복할 때의 성공횟수를 $X$라 하면,
- Parameter : $0 \leq p \leq 1$, $n > 0$;
- MGF : $M_{x}(t)={1+p(e^{t}-1)}^{n}
- x의 p.m.f.
$$f(x)=\begin{pmatrix}n \\ x \end{pmatrix}p^{x}(1-p)^{n-x}, x=0,1,\cdots,n$$
이때 $X$는 모수가 $n$과 $p$인 이항분포를 갖는다고 하고 $X \sim B(n,p)$로 표기한다.
성공확률이 $p$인 베르누이분포는 $n=1$인 이항분포에 해당한다.
- $E(X)=np$
- $Var(X)=np(1-p)$
- $M_{x}(t)=[(1-p)+pe^{t}]^{n}$, $-\infty < t < \infty$
Note : If $Y_{1}, \ldots, Y_{n}$ are underlying Bernoulli RV's then $X=Y_{1}+Y_{2}+\cdots+Y_{n}$(same as counting the number of successes).
Probability function if:
$$p(x) \geq 0, \quad x=0,1,\ldots,n,$$
$$\sum_{x=0}^{n}p(x)=1$$
3. 기하분포(Geometric distribution)
일반적으로 성공확률이 $p$인 베르누이 시행을 처음 성공할 때까지 반복 시행할 때 총 시행횟수를 $X$라 하면,
- x의 p.m.f.
$$f(x)=p(1-p)^{x-1}, x=0,1,2,\ldots$$
이때 X는 모수가 p인 기하분포를 갖는다고 하고 $X \sim Ge(p)$로 표기한다.
-
- $E(X)=\frac{1}{p}$
- $Var(X)=\frac{q}{p^{2}}$
- $M_{x}(t)=\frac{pe^{t}}{1-qe^{t}}$, if $qe^{t} < 1$ or$t <$ -ln $q$
4. 음이항분포(Negative Binomial distribution)
일반적으로 성공확률이 $p$인 베르누이 시행을 $n$번 성공할 때까지 실패한 횟수를 $X$라 하면,
- x의 p.m.f.
$$f(x)=\begin{pmatrix}n+x-1\\ n-1 \end{pmatrix}p^{n}(1-p)^{x}$$
이때 X는 모수가 $n$과 $p$인 음이항 분포를 갖는다고 하고 $X \sim NB(n,p)$로 표기한다.
$n=1$이면 $X \sim Ge(p)$ 가 된다.
또한, $n$개의 독립적인 기하 변수의 합으로 발생하는 것으로 볼 수 있다.
- $E(X)=\frac{r}{p}$
- $Var(X)=\frac{r(1-p)}{p^{2}}$
- $M_{x}(t)=\left[\frac{pe^{t}}{1-(1-p)e^{t}}\right]^{r}$
음이항분포는 성공확률이 일정한 베르누이 시행을 독립적으로 반복한다는 점에서는 이항분포와 동일하나, 이항분포는 일정한 횟수를 시행할 때의 성공횟수의 확률분포인 반면에 음이항분포는 일정 횟수 성공할 때까지의 시행횟수의 확률분포이다.
5. 포아송분포(Poisson distribution)
어떤 실험은 주어진 시간에 혹은 주어진 구간에서 특별한 사건의 발생횟수와 관련이 있다.
-> 셀 수 있는 자료(counting data)는 포아송 분포와 관련이 있다.
- Parameter : rate $\lambda > 0$, $\lambda$는 단위구간에서의 어떤 사건의 발생률이다.
- 길이 1인 구간에서 발생하는 사건의 수 $X$이 p.m.f.를 유도하기 위해 전체 구간을 길이가 같은 $n$개의 부구간으로 나누자.
- 전체 구간에서의 사건의 발생수 $X$는 성공확률이 $\frac{\lambda}{n}$인 근사 베르누이 시행을 $n$번 독립적으로 반복했을 떄의 성공회수(이항분포)로 생각할 수 있다.
$$f(x)=\begin{pmatrix}n\\x\end{pmatrix}\left(\frac{\lambda}{n}\right)^{x}\left(1-\frac{\lambda}{n}\right)^{n-x}$$
- x의 p.m.f. ($x$를 고정시킨 채 $n$을 무한대로 보내면)
$$ f(x)=\frac{e^{-\lambda}\lambda^{x}}{x!}, \quad x=0,1,2,\ldots$$
이때 X는 모수 $\lambda$ $(\lambda \geq 0)$인 포아송분포를 갖는다고 하고$X \sim P(\lambda)$로 표기한다.
- $E(X)= \lambda $
- $Var(X)= \lambda $
- $M_{x}(t)=e^{-\lambda(e^{t}-1)}$
6. 초기하분포(Hypergeometric distribution)
M개의 검은공과 N개의 흰공을 포함하고 있는 항아리가 있다고 하자. M+N개에서 $n$개를 임의 비복원으로 추출할 때 $X$를 선택된 검은공의 개수라고 하자,
- Parameters : $M,N > 0, \qquad 0 < n \leq M+N$
- Possible values : $max(0, n-N) \leq x \leq min(n, M)$
- x의 p.m.f.
$$ f(x)=\frac{ \begin{pmatrix}M\\x \end{pmatrix} \begin{pmatrix}N\\n-x \end{pmatrix} }{ \begin{pmatrix}M+N\\n \end{pmatrix} }$$
이때 $X \sim HG(M,N,n)$로 표기한다.
- $E(X)= np $
- $Var(X)= np(1-p)\left(\frac{N-n}{N-1}\right) $
- $M_{x}(t)= [(1-p)+pe^{t}]^{n}$, $-\infty < t < \infty$
이때 초기하분포의 적률생성함수는 이항분포의 적률생성함수와 동일하다.
적률생성함수가 동일하면, 확률함수도 동일하다.
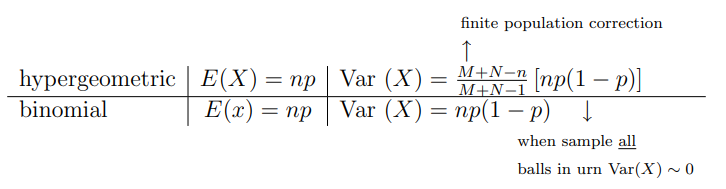
초기하분포의 분산은 이항분포의 분산보다 작음을 알 수 있다.
- 분산은 퍼져있는 정도를 나타내는 데 분산이 작다는 것은 변동성이 적다고 할 수 있다.
- 그 만큼 안정적인 형태라고 볼 수 있다.
- 즉, 초기하분포가 이항분포보다 좀 더 좋은 성질을 가지고 있다는 의미이다.
If we sample with replacement, we would get $X \sim B(n,p=\frac{M}{M+N}).$